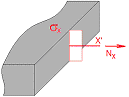
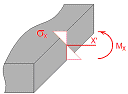
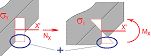
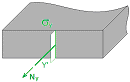
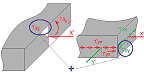
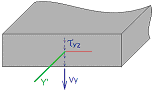
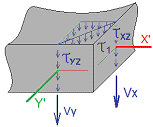
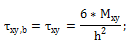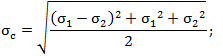Stresses describing bending initiated by loading acting perpendicular to the plane of plate, thermal actions etc.
|
Option |
Action |
Calculation |
Interpretation |
|
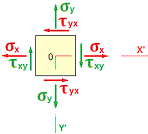
Normal stress is acting the plane perpendicular to the local axis X’ [N/mm2] |
Normal stress due to plane axial force component as a plane stresses state component:
Normal stress due to bending moment component:
2D-Plate package specific (bending only):
2D-Wall package specific (bending + plane stress state):
|
|
|
|
Normal stress is acting the plane perpendicular to the local axis Y’ [N/mm2] |
Normal stress due to plane axial force component as a plane stresses state component:
Normal stress due to bending moment component:
2D-Plate package specific (bending only):
2D-Wall package specific (bending + plane stress state):
|
|
|
|
Shear stress τxy [N/mm2]. Reading rule: shear stress τxy on the local Y’ axis is making shear on the plane is perpendicular to the local X’ axis |
Shear stress due to plane axial force component as a plane stresses state component (plane stress state):
Shear stress due to bending moment component (bending only):
2D-Plate package specific (bending only):
2D-Wall package specific (bending + plane stress state):
|
|
|
|
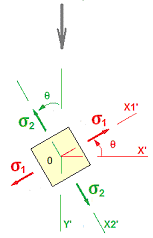
Principle stress σ1 [N/mm2]. Reading rule: Principal stress on the local 1’-axis is acting the cut perpendicular to the local 1’ axis. Local 1’ axis (perpendicular to local 2’ axis) is representing rotated X’ axis where shear stress τxy = τyx vanishes |
Calculated using normal and shear stresses as: 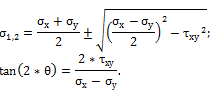
|
|
|
|
Principle stress σ2 [N/mm2]. Reading rule: Principal stress on the local 2’-axis is acting the cut perpendicular to the local 2’ axis. Local 2’ axis (perpendicular to local 1’ axis) is representing rotated Y’ axis where shear stress τxy = τyx vanishes |
Calculated using normal and shear stresses as: 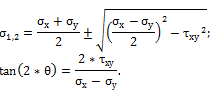 |
|
|
|
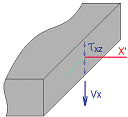
Shear stress τxz [N/mm2] Reading rule: shear stress flow in local Z’ direction is acting the cut is perpendicular to the local X’ axis |
Shear stress due to shear force component 2D-Plate package specific (bending only):
2D-Wall package specific (plane stress state): No results are available
2D-Wall package specific (bending + plane stress state): |
|
|
|
Shear stress τyz [N/mm2] Reading rule: shear stress flow in local Z’ direction is acting the cut is perpendicular to the local Y’ axis |
Shear stress due to shear force component 2D-Plate package specific (bending only):
2D-Wall package specific (plane stress state): No results are available
2D-Wall package specific (bending + plane stress state): 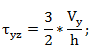 |
|
|
|
Combined shear stress τ1 [N/mm2] |
2D-Plate package specific (bending only):
2D-Wall package specific (plane stress state): No results are available
2D-Wall package specific (bending + plane stress state): 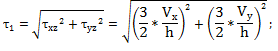 |
|
|
|
|
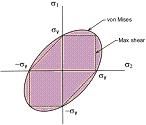
von Mises failure criteria σc [N/mm2] |
Is calculated using principle stresses for 3D problem: 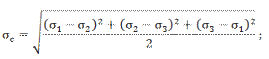
Is calculated using principle stresses for 2D problem:
Is calculated using cartesian stresses for 3D problem:
Is calculated using cartesian stresses for 2D problem:
|
For a plane problem:
|
|
Combined stress (shear stress + normal stress) [N/mm2] |
2D-Plate package specific (bending only)
2D-Wall package specific (bending + plane stress state) |
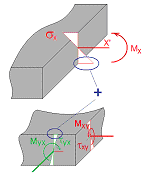
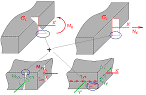 |
|
|
Combined stress (shear stress + normal stress) [N/mm2] |
2D-Plate package specific (bending only)
2D-Wall package specific (bending + plane stress state) |
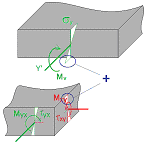
 |