Cross section properties
Cross section definition available in MatrixFrame® consists of:
1. Geometrical properties:
- User defined - basic cross section properties like section area (A), elasticity (E), moment of inertia (I) are calculated and entered manually
- Parametric - cross section properties with opportunity to enter custom section parameters
- Database - cross section properties defined using manufacturer structural shapes database
2. Material properties - cross section material type, available only for parametric and database sections
All geometrical properties are defined and calculated in meters. Geometrical data are validated for incorrect input. After the current cross section is assigned to the structural member the section geometrical and physical characteristics appear in the grid, reverse relationship is impossible.
Cross sections names
Cross section names are generated by different ways. For user defined cross sections you must insert names manually. Parametric cross sections names are generated automatically using short name of section shape and dimensions in millimeters. Database cross sections names are generated automatically by original manufacturer names. For all mentioned cases the possibility to change sections names to your own is available in the grid.
Database cross sections parameters are specified from database by manufacturer settings without ability to modify them. However you can spend some manipulations with them. If section/material name is discretionary changed, it becomes able to modify its parameters and is registered in database as new section/material.
Advanced cross section properties
Several advanced cross section properties are available:
|
Property |
Definition |
Comments |
|
Tapered |
Section begin and end height values are different. Only parametric rectangular cross section may be tapered over height and width simultaneously |
|
|
BiMaterial |
Only parametric rectangular cross section may be defined as BiMaterial (consisting of two materials) |
|
|
Tension |
Structural member is working only for tension, eg. bracing. If tension-only member is compressed, it would be removed from calculations |
By default both Tension and Compression options are active. By excluding Tension and Compression options simultaneously, member is temporary removed from calculations |
|
Compression |
Structural member is working only for compression. If compression-only member is tensed, it would be removed from calculations |
|
|
Cable |
Structural member (only for circular parametric cross sections) is defined as cable influenced (optional) by pre-stressing (the method for overcoming natural weakness in tension) |
|
|
Castellated |
Only I and H shapes cross sections may be defined as castellated. Restriction for castellated cross section: height of castellated cross section must be less than double height of original cross section it is produced from |
Main geometry characteristic values of castellated cross section with hexagonal openings depend on height of original cross section h, height of castellated cross section ht, geometry and positioning of the hexagonal opening. For the Castellated profile branch in the sections DB, geometry relation is defined as following: 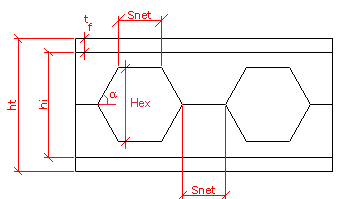
DB section properties are recalculated using described below characteristic geometry values set in DB by using free input. Changing of these values will start recalculation of section property characteristic values and could be the solid base for creation of new cross section families. 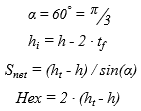 |
|
Density, [kN/m³] |
Mass per unit volume used for self weight calculation |
|
|
Torsional/Polar moment of inertia (It), [m4] |
Moment of inertia used for torsion calculation |
|
|
Second moment of area (Mom. Inn.), [m4] |
The second moment of area (known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia) is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane |
2D-Frame: Mom.Inn depends on cross section rotation angle (for 2D-Frame used angles of 90°-multiplicity), form and dimensions. The rotation angle is formal: considered, that local axes with related characteristics (moments of inertia, loading, etc.) are not rotated, that's why the Mom.Inn switches the values of Iy and Iz according to cross section angle: 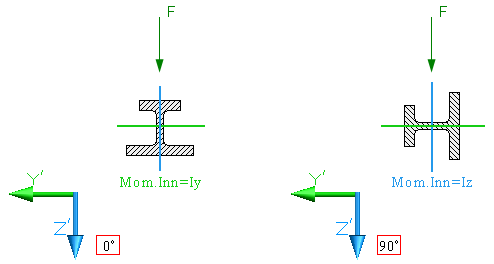
3D-Frame: doesn't change depending on cross section rotation angle about X' axis, because for rotation in 3D-Frame local coordinate system is used - by changing rotation angle the cross section and related characteristics (moments of inertia, loading, etc.) are rotated together with Y' and Z' axes:  |
|
Moment of inertia (Ivv.), [m4] |
Used for stability analysis (for example tension-only elements) as min(Iy, Iz, Iu, Iv)
where: Iu, Iv - moments of inertia related to main coordinate axes u', v' rotated by α angle CCW from the vertical |
|
|
Poisson's ratio (v) |
Ratio, when some object is stretched, of the contraction or transverse strain (perpendicular to the applied load), to the extension or axial strain (in the direction of the applied load) |
Poison's ratio, for example, is used calculating torsional rigidity as GJ by existing torque or performing shear force correction on nodal rotation due analysis of the structure. Here the shear modulus or more commonly the modulus of rigidity G is calculated as: where: E - Young's modulus, [kN/m²] |
|
Shear area (Avy, Avz), [m²] |
Used for the form factor calculation for performing shear force correction on nodal rotation due to analysis of the structure (only if shear force correction in analysis options is enabled) |
Relation between form factor v of the cross section and shear area defined as following: 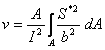 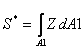
where: Av - shear area of cross section A - total area of cross section
For the rectangular cross section form factor could be calculated as: 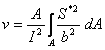 |
|
Pre-stressing, [kN] |
Pre-stressing is working on cable elements only. Pre-stressing as some predefined action on the member is influencing all load cases and combinations. Initial pre-stressing applied on an element indirect is working on element connected members, therefore this action is similar to temperature elongation action |
Pre-stressing as an action used for prefabricated concrete elements has another meaning, where pre-stressing action isn’t distributed over connected members |
Cross sections distribution
Cross sections definition provides sections distribution by member characteristic. There is a difference between 2D-, 3D-Frame and 2D-Grillage, 1D-Beam projects in MatrixFrame®. 2D-, 3D-Frame allow to assign single cross section to member updating the section with a new value, if the new one is assigned to. 2D-Grillage, 1D-Beam allow to assign to member user defined count of sections.