MatrixFrame® beschikt over de optie om te rekenen met elastisch ondersteunde staven. De rekenmethode is gebaseerd op het model van Winkler of het model van Winkler-Pasternak.
Winkler model
De methode Winkler is erop gebaseerd dat de krachten in de elastische ondersteuning evenredig zijn aan de doorbuiging van de staaf. De elastische ondersteuning wordt opgedeeld tot identieke, onafhankelijke, dicht bij elkaar liggende, discrete en lineaire elastische veren. De betreffende constante van evenredigheid van deze veren wordt gezien als veer stijfheidscoëfficiënt Cz, Cy [kN/m³∙m].
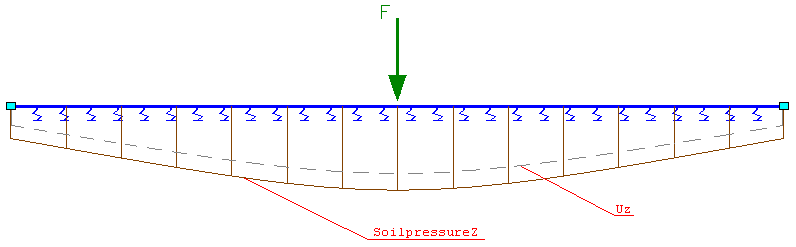
Waarin:
- Gronddruk Z: de gronddruk [kN/m²]
- Uz: verplaatsing [m]
- Cz: Gronddruk Z / Uz: veer stijfheidscoëfficiënt [kN/m³∙m]
Waarbij:
- Voor een 2D vlak wordt gebruikt als veer (grond) stijfheidscoëfficiënt Cz door de Z-as
- Voor een 3D vlak wordt gebruikt als veer (grond) stijfheidscoëfficiënt Cz, Cy door Z- en Y-assen.
Pasternak model
Het rekenmodel volgens Pasternak veronderstelt dwarskrachtinteractie tussen de veren. Dit wiskundig model hanteert de constanten Cfz en Cfy [kN/m]. Deze zijn kenmerkend voor de interactie die optreedt tussen veren die onderhevig zijn aan wrijving vanwege dwarskrachten. Voor de ondergrond heeft Pasternak het model ontwikkeld met twee parameters. Dit model bestaat uit reactiemodel k voor de absorptiecapaciteit van de verticale belasting en reactiemodel G [N/mm] voor de absorptiecapaciteit van de dwarskracht. Pasternak heeft in zijn model de fundering van de grond verdeeld in een toplaag voor horizontale krachten en een laag hieronder voor verticale krachten:
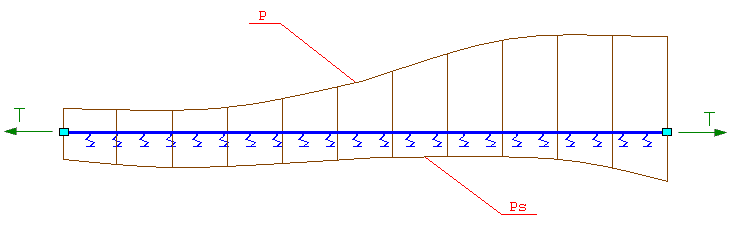
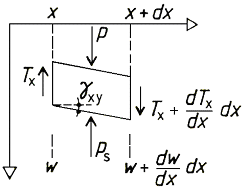
De reactie p van de ondergrond op de ligger volgens de onderstaande vergelijking:
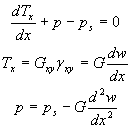
In deze vergelijking is ps=kw eerder genoemd.
De differentiaal vergelijking wordt:
Wanneer:
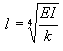 en
en ![]()
Dan:
![]()
![]()
Waarin:
g: dwarskracht ratio
In het geval van een cirkelvormige plaat met axiale symmetrie is de oplossing:
![]()
In het geval van een rechthoekige plaat:
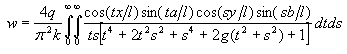
Waarbij:
- Voor een 2D-vlak wordt het veer (grond) stijfheidscoëfficiënt Cfz om de Z as gebruikt
- Voor een 3D-vlak wordt het veer (grond) stijfheidscoëfficiënt Cfz en Cfy om de Z- en Y-assen.
Elastische bedding naam
De naam van de elastische bedding begint standaard met het voorvoegsel 'E' en wordt gevolgd door een nummer. De naam van de Elastische Bedding begint met E1, elke volgende Elastische bedding krijgt het opeenvolgende nummer. Het standaard voorvoegsel kan veranderd worden in de Opties voorkeuren.
Berekeningsmodellen
MatrixFrame® kent twee berekeningsmodellen van de elastische bedding:
-
Lineaire berekening: zonder trekeliminatie
-
Niet lineaire berekening: met trekeliminatie
Beddingsconstante
De beddingsconstante kan op 3 manieren gedefinieerd worden:
-
Cz (veerconstante): uitgaande van een standaard breedte van 1 mtr (optie: GEEN) Hierbij wordt geen breedte in beschouwing. Indien de breedte anders is dan 1 mtr, dient dit in de waarde te worden verdisconteerd.
-
Elastische Bedding constante + profielbreedte: via een op te geven breedtemaat (optie: ABSOLUUT) Hierbij wordt een waarde voor de breedte opgegeven)
-
Elastische Bedding constante (breedte van profiel): de werkende breedte wordt bepaald via de breedte uit de profieleigenschappen (optie: PROJECTIE)
Verlopende elastische bedding
Voor een berekening met een verlopende elastische bedding moeten de begin en de eindwaarden gedefinieerd worden. De waarden dienen derhalve verschillend te zijn.