F-Euler analyse

De F-Euler analyse berekent de factor acr, die de vergrotingsfactor weergeeft waarmee de rekenbelasting vergroot moet worden om een instabiele constructie te krijgen. Theoretisch kan acr berekend worden o.b.v.:

a_cr = F_cr / F_ed

waarin:

F_cr - de elastisch kritische kniklast voor globale instabiliteit, gebaseerd op initiële elastische stijfheden;

F_ed - de rekenbelasting op de gehele constructie.

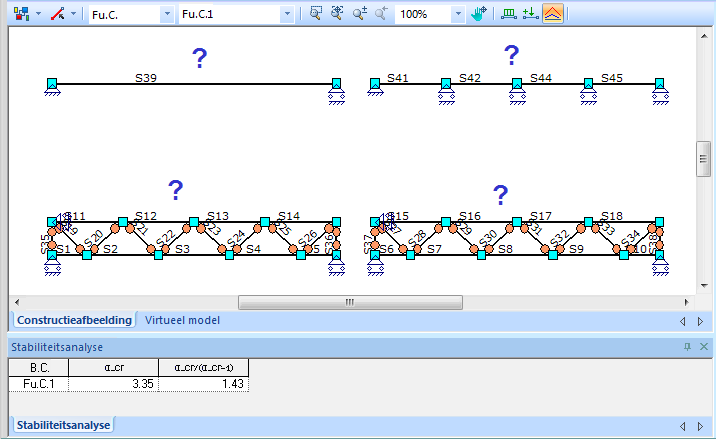
De berekening van de F-Euler stabiliteit wordt in twee stappen uitgevoerd. In eerste instantie wordt een lineaire berekening van de gehele constructie uitgevoerd. Het resultaat hiervan is dat alle vervormingen en krachten, waaronder  de normaalkracht  Nx berekend worden. Hiervan gebruikmakende, wordt vervolgens de F-Euler analyse uitgevoerd.

Bij de berekening van F-Euler wordt aangenomen dat de normaalkrachten in de elementen proportioneel veranderen indien de parameter a>0. De verandering van potentiële energie waarbij de invloed van normaalkrachten aN  van het gehele systeem in rekening gebracht wordt, geeft:

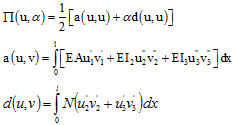                                 (1)

waarin:

P – potentiële energie van een element, rekening houdende met de invloed van de normaalkracht;

E – Elasticiteits modulus (Youngs modulus);

I₂, I₃ – Traagheidsmoment (I₂ = I_z, I₃ = I_y);

u = (u₁, u₂, u₃), v = (v₁, v₂, v₃) – vervormingen:

u₁, v₁ – vervormingen in  Х richting;

u₂, u₃, v₂, v₃ – vervormingen in de hoofdrichtingen van de doorsnede;

l – element lengte.

Afgeleiden in Х' richting:

Gegeven H als een set functies U waarvoor de potentiële energie P(u) kan worden berekend die tevens aan de kinematisch bepaalde randvoorwaarden voldoet. Voor dergelijke randvoorwaarden u v H, gelden de volgende aannames:

a(u, u) > 0                                                                           (2)

Vergelijking (2) beschrijft in feite een geometrisch stabiel systeem. Indien (1) geldt, is het gehele systeem stabiel, wanneer voor alle u v H de volgende vergelijkingen waar zijn:

P(u, a) > 0                                                                           (3)

En het gehele system is instabiel, wanneer voor alle u v H, U ≠ 0:

P(u, a) < 0                                                                           (4)

Verlies van stabiliteit wordt bereikt voor l₀, u₀ v H, u₀ ≠ 0:

P(u_cr, a_cr) = 0                                                                      (5)

Eveneens voor alle a < a_cr moet voldaan worden aan vergelijking (3).

Factor a_cr > 0, conform (5),  wordt het "Stabiliteits kriterium" genoemd. Het stabiliteits kriterium a_cr wordt gebruikt voor de Staal normcontrole (NEN-EN 1993-1-1, EN 1993-1-1 chapter 5.2.1).

Example

Enkel projectbestand dat verschillende separate constructiedelen bevat – kolommen:

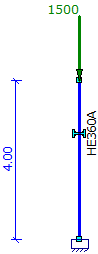
• Berekening van een enkele kolom belast door F=1500 kN:

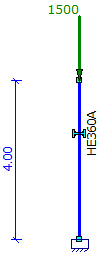
acr = 7.14 < 10 -  GNL berekening is noodzakelijk (NEN-EN 1993-1-1 hoofdstuk 5.2.1)

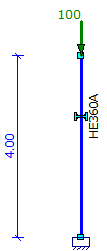
• Berekening van een enkele kolom belast door F=100 kN:

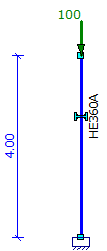
acr= 107.16 > 10 - LE is toereikend (NEN-EN 1993-1-1 hoofdstuk 5.2.1)

• Berekening van een project met twee constructies (deel) – kolommen:

acr = 7.14 < 10 -  GNL berekening is noodzakelijk (NEN-EN 1993-1-1 hoofdstuk 5.2.1)

Conclusie:

Dit is een conservatieve benadering. In het geval van afzonderlijke constructies, bepaalt de maatgevende constructie de term a_cr.

Voor dit onderhavige voorbeeld moet de gehele constructie GNL berekend worden:

1. Alternatief is dat de constructie gesplitst wordt in twee afzonderlijke projecten om het ene deel GNL en het andere deel LE te kunnen berekenen;
2. GNL benadering is altijd beter dan LE voor de normtoetsing staal, de berekening neemt echter wel meer tijd in beslag.