F-Euler analysis

F-Euler calculation performing calculation of factor a_cr by which the design loads would have to be increased to cause elastic instability in a global mode. Theoretical case a_cr is calculating by meaning:

a_cr = F_cr / F_ed

where:

F_cr - the elastic critical buckling load for global instability mode based on initial elastic stiffnesses

F_ed - the design loading on the structure

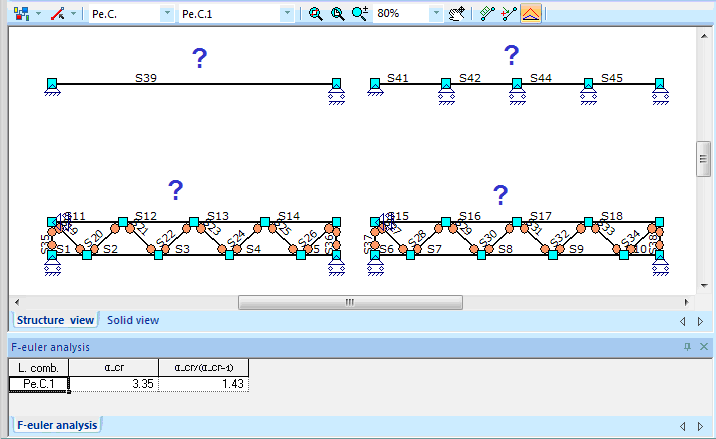
Calculation of F-Euler stability is based on two stages. On the first stage linear calculation of entire system is performed. As result all the forces and displacements including axial forces as  Nx is calculated. Using this calculation of F-Euler is starting.

For the calculation on F-Euler is presumed, that axial force in the elements is changing proportionally the parameter a>0. Changing in potential energy of entire system taken in to account influence of axial forces aN is analyzed:

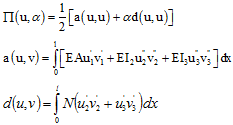                                 (1)

where:

P – potential energy of an element taking in to account influence of axial force

E – Youngs modulus

I₂, I₃ – Moments of inertia (I₂ = I_z, I₃ = I_y)

u = (u₁, u₂, u₃), v = (v₁, v₂, v₃) – displacements:

u₁, v₁ – displacements in Х direction

u₂, u₃, v₂, v₃ – displacements in main directions of cross section

l – element length

Derivatives in Х' direction:

Let define H as set of functions U for that potential energy P(u) could be estimated and that satisfy kinematic determined boundary conditions. Also for such a boundary conditions on u v H, following requirement should be stated as true:

a(u, u) > 0                                                                           (2)

Inequality (2) in fact is describing geometrically stable system. Taking in to account (1), entire system is stable, in case for all u v H following inequality is true:

P(u, a) > 0                                                                           (3)

And entire system is unstable, in case  for all u v H, U ≠ 0:

P(u, a) < 0                                                                           (4)

Loss of stability is met for l₀, u₀ v H, u₀ ≠ 0:

P(u_cr, a_cr) = 0                                                                      (5)

Also for all a < a_cr inequality (3) should be satisfied as true.

Factor a_cr > 0, is satisfying (5), is called "Stability criterion". Stability criterion a_cr is used for Steel code check (NEN-EN 1993-1-1, EN 1993-1-1 chapter 5.2.1).

Example

Single project file calculating different structural parts – columns:

• Calculating single column loaded by F=1500kN:

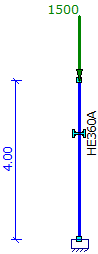
acr = 7.14 < 10 -  GNL calculation is needed  (NEN-EN 1993-1-1 chapter 5.2.1)

• Calculating single column loaded by F=100kN:

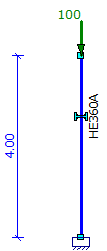
acr= 107.16 > 10 - LE is sufficient (NEN-EN 1993-1-1 chapter 5.2.1)

• Single project calculating two structural elements – columns:

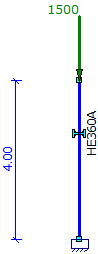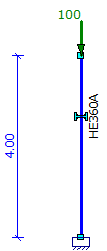acr = 7.14 < 10 -  GNL calculation is needed  (NEN-EN 1993-1-1 chapter 5.2.1)

Conclusion:

Conservative approach is taken. In case of separate structures, the decisive structure part determines a_cr.

For current example the whole structure should be calculated GNL :

1. Otherwise the structure should be split in separate projects to calculate some parts GNL and others LE;
2. GNL approach is always better then LE in case of steel code checking, only calculation is more time consuming.