Finite Element Method
2D-Plate is calculated using Finite Element Method with the basic presumptions as following:
|
Element |
Background |
Convergence of solution |
|
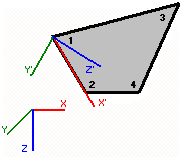
Convex plain 4-nodal thin plate/shell element used for static and free vibrations calculation.
|
Convex plain modified element designed by Fraeijs de Veubeke which correspond theory Kirchhoff (thin plates) is used. Element represents five nodal displacements: X’, Y’, Z’, X’r, Y’r in the local element space and, after global transformation, six nodal displacements: X, Y, Z, Xr, Yr, Zr in the global coordinate space.
Element stiffness matrix is build separately for X’-Y’ (Strain – Stress) and Z’-X’r-Y’r (Bending). Integration in the element – numerical.
Calculation of results as σx, σy, σxy (Stress-Strain), Mx, My, Mxy, Vx, Vy (Bending) is represented in the center of gravity of an element. |
u - displacements; σ - stresses/forces; ||u|| - square root from square of the integral of u in domain of an element;
Means, by refine of meshing net for two times possible error for displacements is decreasing four times, error for stresses (forces) - two times. |
Theories of plates
Depending on the thickness-to-length ratio several theories of plates have been developed:
|
|
Moderately thick |
Thin |
Very thin |
|
t/lx , t/ly |
1/5 to 1/10 |
1/5 to 1/50 |
< 1/50 |
|
Description |
With transverse shear deformation |
Without transverse shear deformation, mostly used for practical applications |
Geometrically non-linear, with membrane deformation |
|
Theory |
Reissner, Mindlin |
Kirchhoff |
von Karman |
|
Related beam theory |
Timoshenko |
Euler, Bernoulli |
Theory of second order |
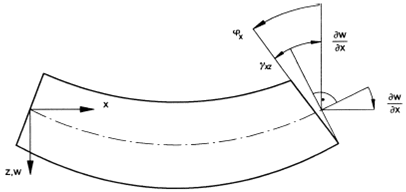
Most of the practical applications deal with thin plates. Within the valid range of linear behavior a pure bending theory will be good enough and shear deformation can be neglected (Kirchhoff theory).
Assumptions of the Kirchhoff plate theory:
- geometrically linear (small strains, small deflections)
- linear material (linear elastic (Hooke), in the most simple case homogeneous and isotrop)
- thin plate
Bernoulli a+b: Kirchhoff theory ![]()
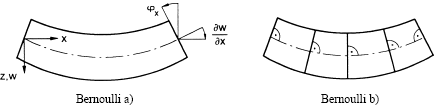
Bernoulli a: Reissner-Mindlin theory ![]()