Steel cross section torsion calculation (bi-moment and St. Venant).
General options:
|
Option |
Unit |
Description |
|
Section |
- |
Cross sections as HEA, IPE etc. are supported by EN1993-1-1 and related national annexes such as NEN-EN 1993-1-1. Items listed in the Section list depend on chosen code or/and national annex |
|
Material |
- |
Steel material name is using for code check calculation and supported by EN 1993-1-1#Table 3.1 and related national annexes such as NEN-EN 1993-1-1#3.1. Items listed in the Material drop down list depend on chosen code or/and national annex |
Torsion calculation input parameters:
|
Parameter |
Unit |
Description |
|
|
L |
m |
Element length |
|
|
TEd |
kNm |
Torsional moment |
|
|
x |
m |
Position |
|
|
|
|
According EN | NEN-EN#6.2.7 stresses in a cross section appears as: |
According NEN 6770#11.2.5 stresses in a cross section appears as: |
|
TB;Ed |
kNm² |
1. Torsional moment bi-moment |
|
|
|
|
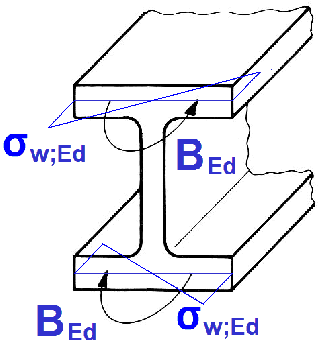
Bi-moment normal stress σw,Ed due to bi-momental bending BEd |
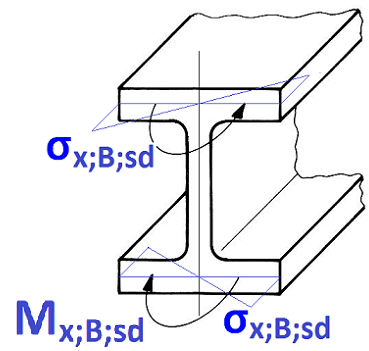
Bi-moment normal stress σx,B,sd due bi-momental bending Mx,B,sd |
|
Tt,Ed |
kNm |
2. Torsional moment St. Venant |
|
|
|
|
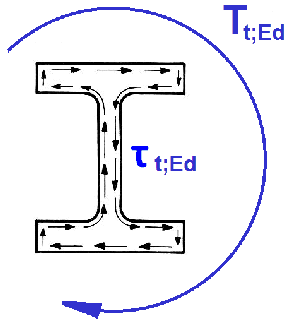
St. Venant shear τt,Ed due to St. Venant torque Tt,Ed |
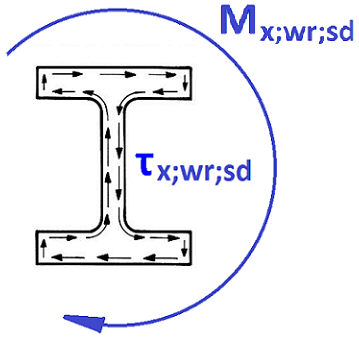
St. Venant shear τx,wr,sd due to St.Venant torque Mx,wr,sd |
|
Tw,Ed |
kNm |
3. Torsional moment warping |
|
|
|
|
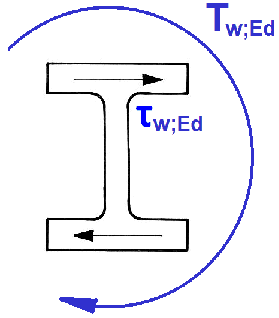
Warping shear in flanges only τw,Ed due to warping torque Tw,Ed |
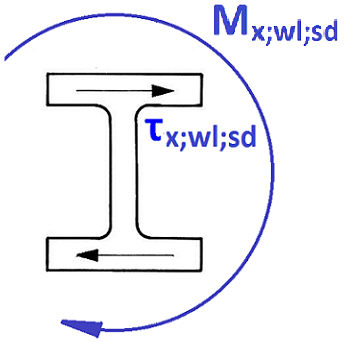
Warping shear in flanges only τx,wl,sd due warping torque Mx,wl,sd |
|
As simplification, in the case of closed hollow cross-section, such as a structural hollow section, it may be assumed that the effects of torsional warping so far bi-momental bending can be neglected.
As simplification, in case of an open cross section, such as I or H, it may be assumed that the effects of St.Venant torque can be neglected.
|
|||
|
UC |
- |
Unity check (UC) is performed using the formula according to EN|NEN-EN1993-1-1#6.2.1(6.1): 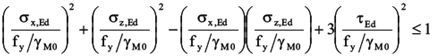
In case σz,Ed=0, the formula according to EN|NEN-EN1993-1-1#6.2.1(6.1) could be reduced to: where: σx,Ed = σw,Ed 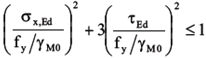 |
Unity check is performed according regulations described in NEN 6770#11.2.5 |
|
Stresses |
- |
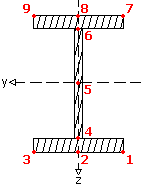
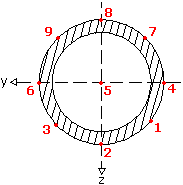
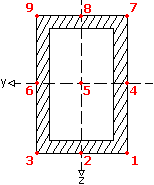
Stresses and unity check (UC) is calculated using MatrixFrame® stress calculation module for 9 decisive points of a cross section as:
The report also provides the maximum UC at all 9 decisive points of a cross-section
|
|