Geavanceerde ponsberekening met koppeling FEM platen.
De positionering van de ponswapening wordt standaard gedefinieerd volgens de "Y"- en "Z"-as vanuit het centrum van de kolom afzonderlijk, respectievelijk op de radiale ("Sr" - de radiale afstand tussen de omtrekken van de wapening) en tangentiële ("St" - de tangentiële afstand tussen de staven) richtingen (Afb. 1) van de omtreklijnen van de wapening:
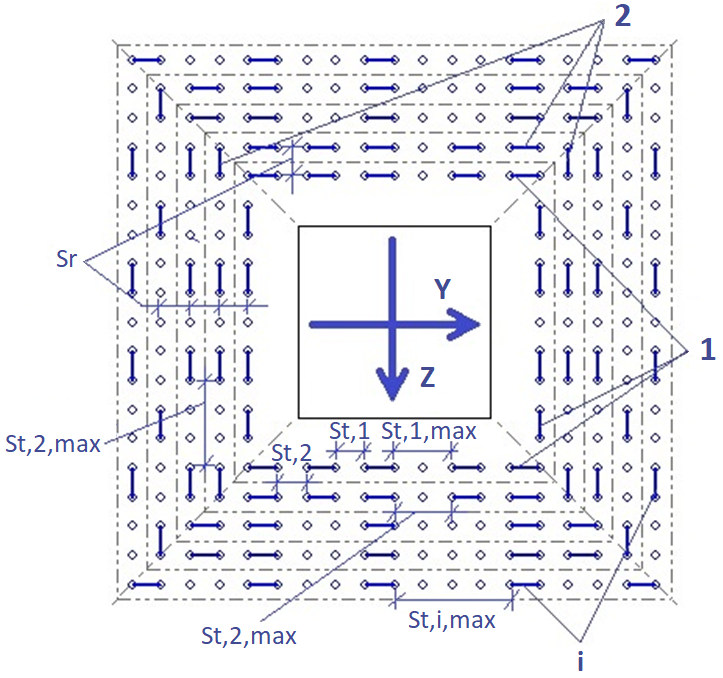
Afb. 1. De afstanden van "Sr" en "St" voor wapening in 2 richtingen
Het wapeningspatroon kan gedefinieerd worden voor de tussen kolom (Afb. 2a), rand kolom (Afb. 2b) of hoek kolom (Afb. 2d) met de mogelijkheid de kolom as te verschuiven t.o.v. de kolomrand (Afb. 2c):
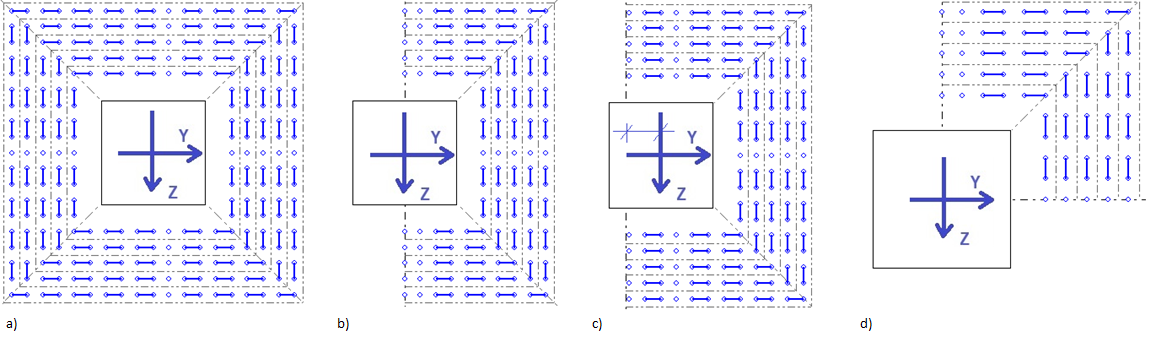
Afb. 2. Kolom positie voor de diverse ponssituaties
De verschuiving genoemd in Afb. 2c kan uitgevoerd worden door handmatige invoer van de "Afstand tot de kolomrand". Deze handeling dient twee keer uitgevoerd te worden indien de kolom gepositioneerd is op de rand van de hoek (Afb. 2d). De wapening die vervolgens getoond wordt in het resultatenscherm is de representatie van het toegepaste patroon "hoek of rand + verschuiving". Voor Afb. 2b "Rand" kolom locatie is de pons wapening 4R6 voor de 1e perimeter loodrecht ten opzichte van de "Y" richting, terwijl de pons wapening voor de 1e perimeter loodrecht ten opzichte van de "Z" richting 2R6 is. Voor Afb. 2c "Rand+verschuiving" kolom positie blijft de pons wapening 4R6 voor de 1e perimeter loodrecht ten opzichte van de "Y" richting, terwijl de pons wapening van 1e perimeter loodrecht ten opzichte van de "Z" richting de waarde 3R6 krijgt.
Het wapeningspatroon kan toegepast worden in radiale richting "Yr" of "Zr" (Afb. 3a), twee richtingen "YZ" of ZY" (Afb. 3b), of een enkele richting "Y", "Z" (Afb. 3c), waarbij dezelfde regels gelden voor een patroon in Y of Z:
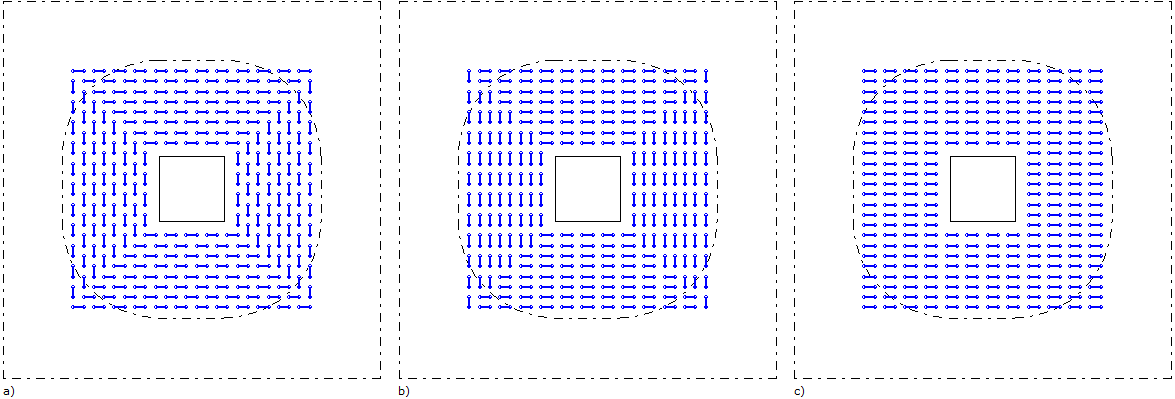
Afb. 3. Ponswapeningspatroon
Een algemeen toegepast radiaal "Yr" of "Zr" (Afb. 3a) of twee richtingen "YZ" of "ZY" (Afb. 3b) patroon kan op detailniveau aangepast worden in het resultaten scherm, gebruikmakend van de droplist voor beugelrichting (Afb. 4).
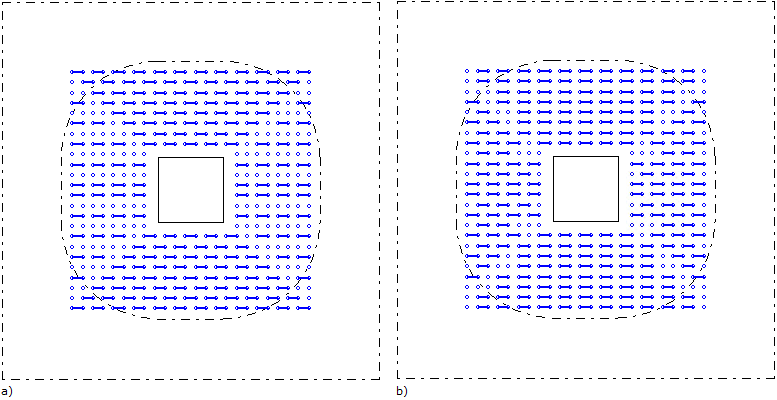
Afb. 4. Gemengde vorm van het pons wapening patroon voor radiale en twee richtingen situaties
Toepassen van de pons wapening reductie met behulp van de "Reductie" vlag, waarbij het aantal beugels van de 1e perimeter hetzelfde is voor de overige perimeters (Afb. 5):
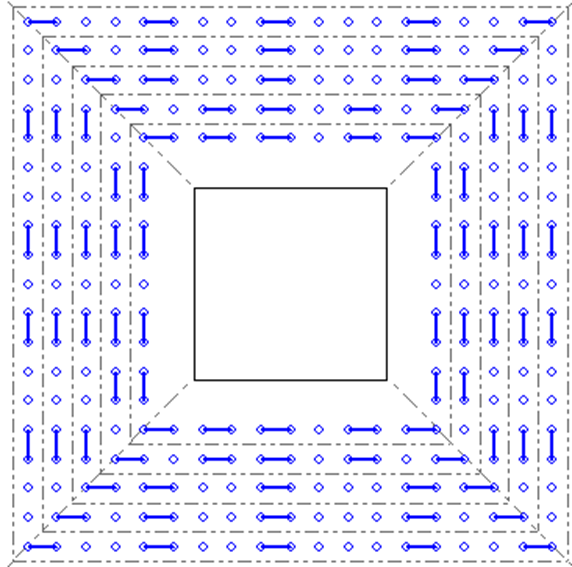
Afb. 5. Gereduceerde pons wapening situatie (voor een radiaal patroon)
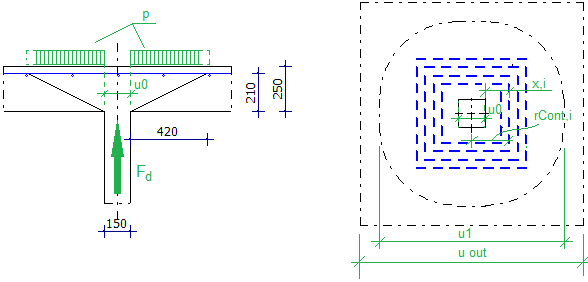
Afb. 6. Positie van het belaste gebied
Selectie van toe te passen patronen, aanpasbare wapeningspatronen alsmede wapeningsreductie is alleen mogelijk voor de geavanceerde Pons berekening (Technische module No. 387).
De dwarskracht VEd wordt berekend als VEd = Fd – A ⋅ p (Afb. 6), waarin het gebied A (Afb. 5) wordt berekend exclusief het belaste gebied u0 voor alle perimeters. VEd is aan te passen in de geavanceerde ponsmodule.
Detaillering regels en limiteringen van beugelspelden worden beschreven in de EN1992-1-1#9.4.3 (1):
- Beugels dienen op zijn minst 2 perimeters te hebben, en voor opgebogen wapening geldt dat ze 1 perimeter moeten hebben;
- Controle op afstanden Sr < Sr,max = 0.75d is alleen van toepassing op beugels, dus in geval van opgebogen staven blijft deze controle achterwege.
Volgens de EN1992-1-1#9.4.3 (Afb. 9.10b) is de afstand tussen opgebogen wapening aan onderzijde ongeveer 2d, een exacte check is dus niet mogelijk op "ongeveer". Tevens zijn er volgens de EN1992-1-1#9.4.3 (4) alleen regels voor controle voor de bovenkant.
Het vereiste aantal wapeningsperimeters, aangegeven door "Volgend" geeft aan dat de positie van de betreffende perimeter nog niet voldoet aan de controle xi < (uout – kd). Indien de perimeter buiten de vereiste positie ligt wordt dit aangegeven met het "Stop" teken en geeft aan dat wapening in volgende perimeters overtollige is.
Voor opgebogen wapening zijn er geen eisen voor de lengte van de horizontale takken van de betreffende opgebogen wapening. De getoonde horizontale stukken in de presentatie zijn dan ook indicatief:
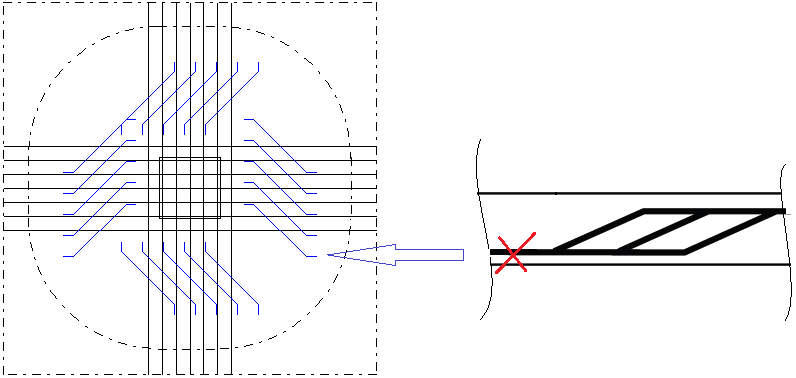
De ponsweerstand van platen zonder ponswapening is afhankelijk van de verhouding van de langswapening (netten, wapeningsstaven) (NEN-EN 1992-1-1 #6.4.4). In de gebruikersinterface kunnen wapeningsnetten worden aangeboden, samen met extra wapeningsstaven (bijvoorbeeld: R10-200+10R12). Bij de berekeningen van de wapeningsverhouding wordt rekening gehouden met de oppervlakte van de staven, samen met het wapeningsnet. Er wordt aangenomen dat wapeningsstaven worden verlengd en verankerd buiten de uout-omtrek.
In de module 'Ponsberekening geavanceerd' kunnen naast de parametrische cirkelvormige en rechthoekige kolomdoorsneden, die vaak worden gebruikt voor reguliere ponsberekeningen, nu ook nieuwe doorsneden zoals rechthoekboog, veelvlak en T-vorm worden gebruikt. Gedetailleerde beschrijvingen van de parameters voor deze doorsneden zijn beschikbaar in Parametrische profielen.
De β-factor wordt gebruikt om de effectieve ponsomtrek aan te passen om rekening te houden met een niet-uniforme schuifkrachtverdeling, met name wanneer de kolom excentrisch wordt belast of niet symmetrisch ten opzichte van de plaat is geplaatst.
De 'Ponsberekening' / 'Ponsberekening geavanceerd'-module biedt verschillende opties voor het berekenen van de β-factor:
- Geen excentriciteit: de β-factor wordt ingesteld op 0;
- Standaard β volgens Afb. 6.21N: β-factoren worden toegepast volgens NEN-EN 1992-1-1#6.4.3 (Afb. 6.21N);
- Laterale stabiliteit afhankelijk van raamwerking: de β-factor wordt berekend op basis van NEN-EN 1992-1-1#6.4.3(3) met gebruik van door de gebruiker gedefinieerde waarden voor My,Ed en Mz,Ed;
- Algemene methode: De β-factor wordt berekend volgens de methodologie beschreven in de artikelen "Cement: Ponsberekening nader beschouwd (Normbesef 1)," maart 2023 en "Durchstanznachweis nach EC2" door Prof. Dr.-Ing. Rudolf Baumgart (5-10-2020). Deze methode levert de volgende berekende β-factor op:
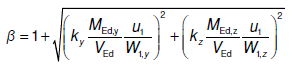
De algemene methode is exclusief beschikbaar in de module 'Ponsberekening geavanceerd'.
Voor hoekkolommen kunnen de plaatranden een hoekrotatie vormen met het orthogonale coördinatensysteem.

Deze functie is ook alleen beschikbaar in de module 'Ponsberekening geavanceerd'.